Nonlinearity is a fundamental concept in various scientific disciplines, describing the behavior of complex systems where the relationship between cause and effect is not proportional. In simpler terms, nonlinearity refers to situations where small changes in input can lead to disproportionately large changes in output, making the system unpredictable and highly sensitive to initial conditions. This concept finds applications in diverse fields, from mathematics and physics to engineering, economics, and even proxy server technologies.
The history of the origin of Nonlinearity and the first mention of it.
The study of nonlinearity can be traced back to ancient times when philosophers and scholars observed that some natural phenomena did not follow linear patterns. However, the formalization of the concept began to take shape in the late 19th and early 20th centuries. Pioneering work in chaos theory by mathematician Henri Poincaré and meteorologist Edward Lorenz significantly contributed to the understanding of nonlinearity.
Henri Poincaré’s work on the three-body problem in celestial mechanics revealed that the behavior of three mutually interacting celestial bodies could lead to unpredictable, non-periodic trajectories. This marked the emergence of chaotic behavior in mathematical systems. Edward Lorenz’s groundbreaking research on atmospheric convection discovered that minor changes in initial conditions could have a substantial impact on weather predictions. His famous “butterfly effect” analogy illustrates how small atmospheric changes can lead to significant weather variations.
Detailed information about Nonlinearity: Expanding the topic Nonlinearity
Nonlinear systems exhibit unique characteristics that distinguish them from linear systems. In a linear system, the principle of superposition holds, meaning the combined response of inputs is the sum of their individual responses. In contrast, nonlinear systems defy this principle, leading to intricate and often unpredictable behavior.
Nonlinearity can arise from various sources, such as feedback loops, time delays, and threshold effects. The presence of feedback loops, where the output influences the input, can introduce self-reinforcing or self-damping behavior. Time delays in system responses can lead to oscillations and instability. Threshold effects imply that a system may remain inactive until a certain threshold is crossed, triggering sudden and dramatic changes.
The internal structure of Nonlinearity: How Nonlinearity works
Nonlinearity is embedded in the very fabric of complex systems. It emerges from the interactions and relationships between individual components within the system. Understanding the internal structure of nonlinearity often involves mathematical tools such as differential equations, fractals, and bifurcation diagrams.
Fractals are intricate geometrical patterns that repeat themselves at different scales, offering insights into the self-similarity and complexity of nonlinear systems. Bifurcation diagrams help visualize how a system’s behavior changes as a parameter is varied, highlighting the emergence of multiple stable states and chaos.
Analysis of the key features of Nonlinearity
Nonlinearity is characterized by several key features that set it apart from linear behavior:
- Sensitive Dependence on Initial Conditions: Nonlinear systems are highly sensitive to their starting conditions, making long-term predictions challenging or impossible.
- Bifurcations and Multiple Equilibria: Nonlinear systems can undergo bifurcations, where small changes in parameters lead to the emergence of new stable states or periodic behavior.
- Strange Attractors and Chaos: Some nonlinear systems exhibit strange attractors in phase space, representing long-term behavior that is neither periodic nor convergent.
- Long-Tail Distributions: Nonlinear systems often display long-tail distributions, where rare events have a significant impact on the overall system behavior.
- Emergence and Self-Organization: Nonlinear systems can exhibit emergent properties, where complex behavior arises from simple interactions between components.
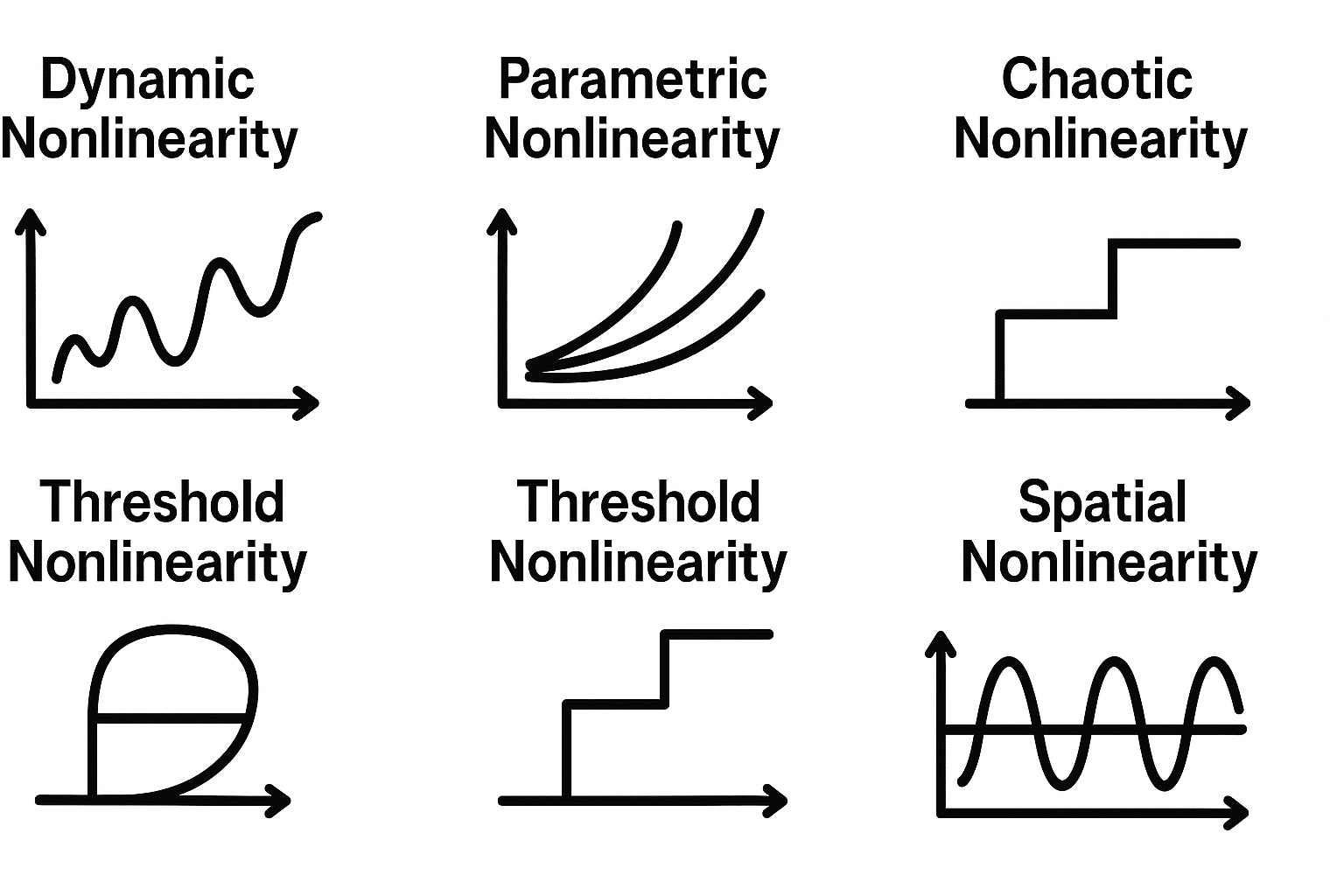
Types of Nonlinearity
Nonlinearity manifests in various forms across different fields. Here are some types of nonlinearity:
| Type | Description |
|---|---|
| Dynamic Nonlinearity | System behavior changes over time. |
| Parametric Nonlinearity | System behavior changes with varying parameters. |
| Chaotic Nonlinearity | Highly sensitive to initial conditions and exhibits chaotic behavior. |
| Threshold Nonlinearity | Only responds once a threshold is crossed. |
| Hysteresis Nonlinearity | Depends on the history of inputs and outputs. |
| Spatial Nonlinearity | Behavior varies with spatial location. |
Applications of Nonlinearity
- Chaos Theory and Weather Prediction: Understanding chaos and nonlinearity has improved weather prediction models, making them more accurate and reliable.
- Economics and Finance: Nonlinear dynamics help model complex economic systems, including stock market fluctuations and business cycles.
- Engineering and Control Systems: Nonlinearity is essential for designing robust control systems in aerospace, robotics, and other engineering domains.
Challenges and Solutions
- Prediction and Uncertainty: Nonlinearity makes long-term predictions challenging. Techniques like ensemble forecasting and data assimilation help mitigate uncertainty.
- Optimization and Search: Finding optimal solutions in nonlinear systems can be difficult. Evolutionary algorithms and simulated annealing are used for optimization.
- Stability and Control: Nonlinear systems can exhibit instability. Lyapunov stability analysis and adaptive control are used to ensure stability.
Main characteristics and other comparisons with similar terms
| Characteristic | Nonlinearity | Linearity |
|---|---|---|
| Response to Inputs | Disproportional | Proportional |
| Principle of Superposition | Not applicable | Applicable |
| Sensitivity to Initial Conditions | Highly sensitive | Insensitive |
| Behavior | Complex, unpredictable | Predictable, stable |
The study of nonlinearity continues to evolve, promising exciting future prospects in various fields:
- Artificial Intelligence: Nonlinear techniques, like neural networks, are revolutionizing AI and machine learning, enabling sophisticated pattern recognition and decision-making.
- Climate Science: Nonlinearity plays a vital role in climate models, and a better understanding will aid in predicting and mitigating the impacts of climate change.
- Network Dynamics: Studying nonlinearity in complex networks can enhance our understanding of social, biological, and technological interactions.
How proxy servers can be used or associated with Nonlinearity
Proxy servers, like those offered by OneProxy, can benefit from an understanding of nonlinearity. As intermediaries between clients and servers, proxy servers handle requests and responses. Nonlinearity may arise in:
- Traffic Analysis: Nonlinear techniques can help in understanding varying user behavior, preventing attacks, and improving security.
- Load Balancing: Nonlinearity in user requests can necessitate adaptive load balancing algorithms to ensure optimal server performance.
- Caching: Nonlinear patterns in user access can inform intelligent caching strategies, reducing response times and bandwidth usage.
Related links
To delve deeper into the concept of nonlinearity, check out these resources:
- Chaos: Making a New Science by James Gleick
- Nonlinear Dynamics and Chaos by Steven H. Strogatz
- Introduction to the Theory of Nonlinear Optimization by Johannes Jahn
In conclusion, nonlinearity is a captivating and vital aspect of complex systems that defies simple cause-and-effect relationships. From ancient philosophical ponderings to modern scientific investigations, the concept has evolved significantly, finding applications in numerous fields, including proxy server technologies. As our understanding of nonlinearity advances, it opens up new avenues for innovation and problem-solving across various disciplines.